Sin da piccoli ci è stato insegnato il mantra per calcolare l’area del cerchio, quel “raggio per raggio per 3 e 14” che ci accompagna per tutta la vita. Finché si è bambini non ci si interroga troppo e si è portati a fidarci dei grandi, quindi “3.14” non causa poi troppi pensieri, anche perché tutto sommato funziona. Ma poi viene il momento in cui ci si chiede da dove salti fuori.
Da qui in poi scriverò π per indicare “pi greca”, com’è normale fare trattandosi appunto della lettera ‘p’ dell’alfabeto greco, scelta perché iniziale del termine περιφέρεια (letto periferéia) che significa ‘circonferenza’. Questo simbolo è apparso come costante numerica sin dall’antichità (1) quando si tentò di mettere in relazione la circonferenza di un cerchio e il suo diametro. Allora spesso le misure erano effettuate con una fune e in questo caso la fune veniva srotolata dal cerchio e poi messa in relazione con una cordicella posta sul diametro. Possiamo usare lo stesso metodo anche oggi che conosciamo il numero zero e abbiamo a disposizione il righello, vedremo che la misura è più agevole di allora ma il risultato non cambia, come rappresentato in Figura 1:

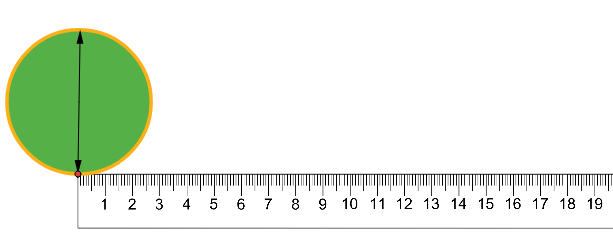
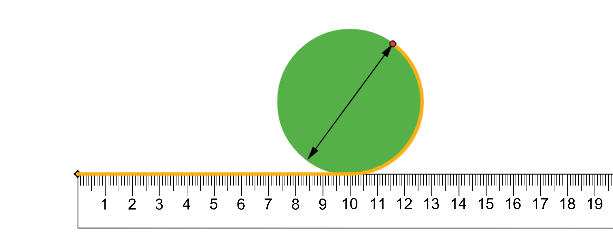
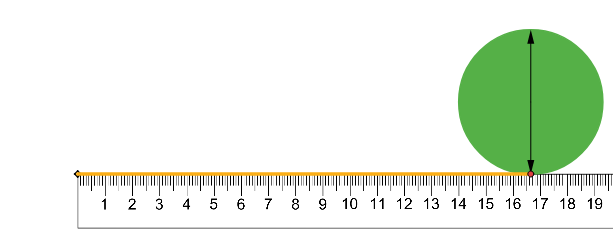
Figura 1. Il metodo più antico per misurare gli oggetti e quindi anche il perimetro e il diametro del cerchio fa uso di una fune (gialla nelle immagini) che viene srotolata e confrontata con un’altra posta sul diametro (doppia freccia nera).

Fece così la sua comparsa sulla scena questo numero, un po’ scomodo perché con la virgola e quindi difficile da misurare con grande precisione:

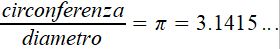
‘π’ è dunque una costante ed è un numero irrazionale, cioè non esiste una frazione che lo identifichi. Ad esempio, mentre il numero 0.625 è pur esso con il punto decimale ma può essere scritto come 5/8 se questo ci semplifica la vita, lo stesso è impossibile fare per π sebbene esistano alcune frazioni che lo approssimano alle prime cifre decimali, come ad esempio 25/8 o meglio 22/7.
Del calcolo di π si occupò già intorno al 250 a.C. Archimede. La sua Scuola Pitagorica aveva scoperto da poco il concetto di infinito che oggi giorno è di uso comune (anche se in pochi ne percepiscono il significato reale e profondo) ma che allora fu una novità sensazionale e, per chi studiava scienza e filosofia, persino traumatica. Scoprì l’infinito grazie al connubio esistente fra stella e pentagono, evidenziando che se si uniscono diagonalmente i vertici di una stella, al suo interno si forma un pentagono, come in Figura 2. Unendo i vertici del pentagono, si forma al suo interno una nuova stella più piccola. Unendo i vertici di questa stella più piccola nasce un nuovo e più piccolo pentagono, e così via. I Pitagorici realizzarono che questa sequenza non avrebbe mai avuto fine, per quanto a un certo punto sarebbe diventato arduo riuscire a disegnare le due figure geometriche a causa delle loro risicate dimensioni. Ma sarebbe stato un mero impedimento pratico, non di principio. E fu così che il concetto di infinito fece il suo clamoroso ingresso nella Conoscenza umana con tutte le implicazioni anche filosofiche che di lì a poco sarebbero emerse, anche già fra i Pitagorici stessi, che non a caso fecero della stella connessa a cinque punte il ‘logo’ della Scuola Pitagorica.

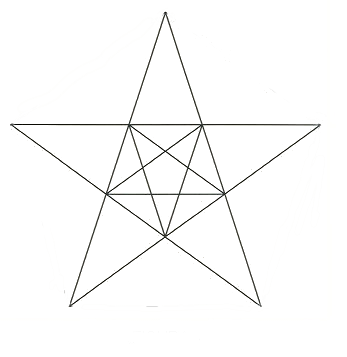
Figura 2. Figura 2. Immagine che permise ai Pitagorici di introdurre il concetto di infinito. Unendo le punte della stella e i vertici del pentagono si formano rispettivamente nuovi pentagoni e nuove stelle, con un processo che non ha mai fine..

Con questo nuovo e importante concetto, Archimede fu in grado di elaborare molte nuove idee. Trovò così una strategia davvero brillante per calcolare π. Rimpiazzò il cerchio con una figura molto più comoda, un poligono con molti piccoli lati e poi raddoppiò il numero di lati e poi ancora, per avvicinarsi alla perfetta rotondità del cerchio. Ma la cosa stupefacente è che invece di farlo in modo casuale, accontentandosi di raggiungere un’accuratezza non-nota, metodicamente costruì un sandwich intorno al cerchio, dove le fette di pan carré erano poligoni rispettivamente inscritti e circoscritti al cerchio come visibile in Figura 3:

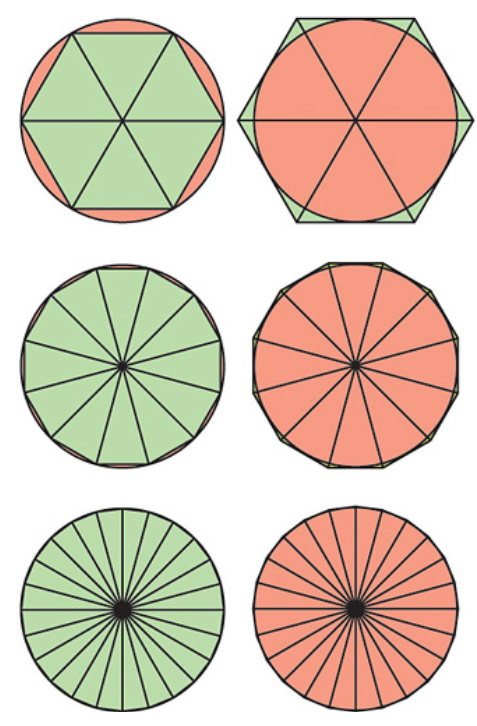
Figura 3. Partendo dall’alto, una prima approssimazione del cerchio è ottenuta con un esagono (in verde). Nella parte a sinistra l’esagono è inscritto nel cerchio, in quella a destra è circoscritto. Le parti residue visibili, rosa a sinistra e verdi a destra fanno percepire che l’esagono è una cattiva approssimazione del cerchio, ma è un buon inizio.
Raddoppiando i lati e portandoli a 12 come nella figura centrale, le cose vanno molto meglio e la differenza fra le figure e il cerchio è appena percettibile ad occhio.
Meglio ancora raddoppiando ancora e costruendo le due figure a 24 lati, in basso, che forniscono una buona approssimazione del cerchio contenuto fra i due poligoni.

Archimede proseguì con 48 e poi con 96 lati, utilizzando il Teorema di Pitagora per calcolare i perimetri di queste figure complesse e rapportandole al diametro del cerchio. Con questo metodo riuscì a dimostrare che π è compreso fra due numeri ben precisi:

che, svolgendo le divisioni delle frazioni, corrisponde a:

un risultato eccezionale per l’epoca. Questo “metodo dell’esaurimento” (exhaustion method) è molto ingegnoso puntando sul confinare il cerchio fra due figure più semplicemente trattabili (al tempo) dal punto di vista geometrico. Ancora oggi è utilizzato in Analisi Matematica soprattutto per il calcolo dei limiti di una funzione.
Ma la vera novità e grandezza del metodo di Archimede deriva da quel concetto di infinito di cui abbiamo detto poche righe sopra, appena scoperto dai Pitagorici stessi: procedendo appunto all’infinito col raddoppio dei lati il risultato del rapporto fra i perimetri delle figure e il diametro del cerchio converge esattamente a π. Ciò significa che il metodo è assoluto e che è sufficiente scegliere il giusto numero di lati della figura inscritta e di quella circoscritta per riuscire a calcolare π con il numero desiderato di cifre decimali.

L’evidenza pitagorica che π non è un numero algebrico e che non si può rappresentare con una semplice frazione ha, fra l’altro, sancito l’impraticabilità di un problema molto famoso e sul quale nel tempo si sono scervellati centinaia di matematici: la famosa “quadratura del cerchio”. Si tratta di costruire un quadrato che abbia la stessa area di un determinato cerchio usando unicamente riga e compasso.
Questa “impraticabilità” è stata dimostrata essere una “impossibilità” soltanto nel 1882 quando il matematico tedesco Ferdinand von Lindemann pubblicò la dimostrazione (3) che π è un numero trascendente. Siccome l’area del cerchio è  allora un quadrato con questa stessa area deve avere lato pari a  ovvero  Ma siccome π è un numero trascendente, anche  lo è, il che rende non-costruibile il quadrato con questo lato.
È curioso che nell’uso comune si usino espressioni come “abbiamo trovato la quadratura del cerchio” per indicare che si è scovata la soluzione perfetta ad un certo problema, usando un termine di paragone che come abbiamo visto …non esiste.

Dato che la quadratura del cerchio non riusciva a nessuno, dai tempi di Archimede in poi si è scatenata una vera e propria gara per individuare il maggior numero di cifre decimali corrette di π. Fino agli inizi del ‘900, tuttavia, il numero di cifre decimali dimostrate corrette non era stratosferico. Nel 1873 William Shank usò una formula per ricavare π trovata nel 1706 da John Machin (2) e mediante calcoli fatti ovviamente a mano riuscì a ricavare il ragguardevole numero di 527 decimali, un record che rimase imbattuto fino al 1946, quando Ferguson e Wrench, utilizzando una sorta di calcolatore elettromeccanico ricavarono i primi 1120 decimali.
Arrivò poi l’era dei calcolatori digitali e il numero di decimali si impennò clamorosamente fino ad arrivare all’incredibile numero di 2.0211229×1014 di fine giugno 2024. Quanto i calcolatori digitali abbiano contribuito in questa corsa è evidente dal grafico di Figura 4 che riporta in ascissa il tempo in anni a partire da prima di Cristo fino ai giorni nostri e, in ordinata, il numero di decimali corretti noti. Impossibile non rimanere colpiti dalla brusca impennata che ha il grafico a partire dal secolo scorso, quando appunto hanno fatto la loro comparsa sulla scena i calcolatori digitali e, con loro, algoritmi sempre più sofisticati per il calcolo dei decimali di π.

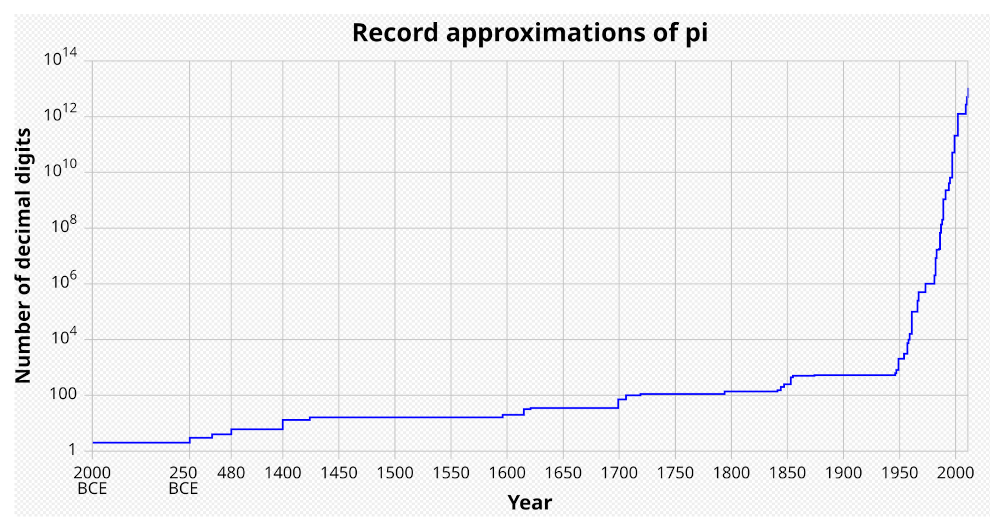
Figura 4. Andamento negli anni del numero di decimali di π conosciuti con certezza. In ascissa ‘BCE’ è una dicitura anglosassone (Before Common Era) per a.C. e indica gli anni prima di Cristo. Si noti che l’ordinata è in scala logaritmica, per poter racchiudere il grafico in un’area ragionevole. Se la scala fosse stata lineare sarebbe servito un rotolo di carta igienica per disegnarlo.

Ma questa corsa ha senso ? Quanti decimali di π servono davvero per fare i conti?
Per rispondere a queste domande non ci si deve concentrare su quale valore reale assegnare a π durante i calcoli, ma piuttosto su quale errore si commette nel risultato finale non utilizzando un numero maggiore di cifre decimali. Ovviamente, tanto più grande è il cerchio considerato, tanto più grande è l’errore commesso, se utilizziamo un numero troppo basso di decimali. E allora riferiamoci al cosmo (4) … sarà un conto divertente con un risultato sorprendente (e confortante).
Consideriamo ad esempio l’oggetto creato dall’uomo oggi più distante dalla Terra, la sonda spaziale Voyager 1, lanciata verso i confini del cosmo nel 1977 (è la sonda che scattò la famosa fotografia chiamata “Pale blue dot” al nostro pianeta da una distanza di 6 miliardi di chilometri, una foto molto poetica in cui il piccolo pallino azzurro del nostro pianeta brilla nel buio).
Da allora Voyager 1 si è allontanata circa 24 miliardi di chilometri da noi. Consideriamo l’incredibile cerchio che abbia questa distanza come raggio, vale a dire circa 48 miliardi di chilometri di diametro e calcoliamone il perimetro: circa 151 miliardi di chilometri.
Se facciamo il calcolo utilizzando 15 decimali anziché il valore “vero” di π commettiamo un certo errore sul valore finale del perimetro rispetto a quello che è in realtà. Ebbene si può dimostrare che questo errore è di appena 1 centimetro. Questo merita una riflessione attenta: un cerchio con perimetro di 151 miliardi di chilometri e la nostra misura ha un’imprecisione per la lunghezza dell’unghia del nostro mignolo !
Quel ‘15’ non è stato scelto a caso, è il numero di decimali di π che gli scienziati utilizzano per fare i conti cosmologici. E per fare conti con distanze e lunghezze più ridotte di quelle, ne bastano molti meno. Quindi la gara a trovare il maggior numero di decimali corretti di π è da considerarsi un mero esercizio matematico che è di nessuna utilità pratica in Fisica e in Ingegneria.
Che π abbia affascinato l’intelligenza umana, solleticato l’immaginazione e da sempre occupato un posto privilegiato nella Conoscenza lo dimostrano non soltanto gli innumerevoli scritti in ambito matematico e scientifico, ma anche riferimenti nell’arte e nella letteratura. Persino il sommo Dante cita il problema della quadratura del cerchio nell’ultimo canto del Paradiso:

Qual è ’l geomètra che tutto s’affige

per misurar lo cerchio, e non ritrova,

pensando, quel principio ond’ elli indige,

tal era io a quella vista nova.

Qui “principio” sta proprio per l’annoso problema, che al tempo di Dante era difficile e impraticabile, ma che oggi sappiamo essere impossibile.
Il numero π continua ad affascinare a tal punto che gli è stato dedicato un particolare giorno del calendario. Il pi day si celebra il 14 Marzo, che in notazione anglosassone si scrive anteponendo il mese al giorno: 3,14 appunto, un meritevole riconoscimento ...sebbene si limiti alle sole due prime cifre decimali.
Ma c’è chi fa di peggio: nell’insieme delle battute ‘nerd’ circa la crescente imprecisione dei Matematici, dei Fisici e infine degli Ingegneri si annovera anche l’accusa rivolta a questi ultimi di fare approssimazioni notoriamente ardite, inconcepibili per i primi e mal sopportate dai secondi. Sta di fatto che quando serve calcolare in fretta l’ordine di grandezza della soluzione finale, per gli Ingegneri a volte basta anche un π=3 :-)

Marco Sartore

(1) “A History of Pi “, Petr Beckmann, 3rd ed., St. Martins Press, 1974.

(2) “Modular Equations, and Approximations to Pi, or How to Compute a Billion Digits of Pi”, American Mathematical Monthly 96, 3 (1989)

(3) “Lindemann”, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.

(4) EDU News, Jet Propulsion Laboratory magazine, Oct 24, 2022.