Per la media delle persone, avventurarsi a leggere qualcosa a proposito della famosa “Relatività di Einstein” è considerata un’impresa titanica che solitamente fa desistere ancor prima di iniziare.

Io invece mi auguro che si vada oltre queste credenze popolari e che leggiate oltre queste prime righe perché qui non ci saranno chissà quali astruse formule, bensì solo concetti semplici ma “geniali” come colui che li postulò all’inizio del secolo scorso. E anch’egli lo fece utilizzando costrutti matematici di base, come in tutta la trattazione della sua “Relatività ristretta” (quella che non considera l’accelerazione dei corpi in moto) dove Einstein utilizzò quasi esclusivamente l’algebra, regalando al mondo un’opera di una bellezza straordinaria, anche appunto per la sua sconcertante “semplicità”.

Anche io voglio usare in questo articolo un unico concetto molto semplice, che il cartello stradale del limite di velocità ci ricorda ogni volta: quel “50” dentro al cerchio rosso significa chilometri all’ora ed è la velocità massima consentita in quel tratto di strada. Dunque la velocità si calcola dividendo lo spostamento (che nel cartello si misura in chilometri) per il tempo impiegato a percorrerlo (che nel cartello si misura in ore).

In poche parole quel cartello stradale contiene la formula che lega velocità a spostamento e tempo:

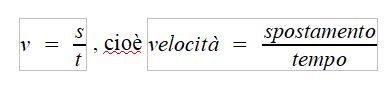
E veniamo al punto. Tutta la trattazione di Einstein è basata su due soli postulati:
1) gli esperimenti danno i medesimi risultati se effettuati da fermi oppure in movimento
2) la velocità della luce, che indichiamo con la lettera c e vale circa 300.000 km/s, è sempre la stessa per ogni osservatore fermo o in moto.

Basandosi su questi due soli postulati Einstein si chiese: che succede ad un orologio quando viaggia molto veloce?
Per capirlo consideriamo un meccanismo molto semplice, che emette un raggio di luce il quale colpendo uno specchio emette un “tick”, poi torna indietro e viene rilevato da un sensore che emette un “tock”, come in figura 1:

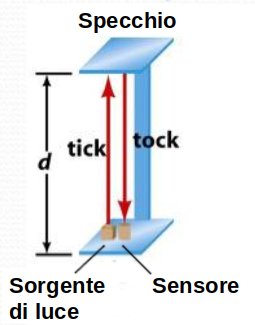
Figura 1: “orologio a raggio di luce” fermo rispetto a noi osservatori esterni, in cui il tick-tock avviene ogni volta che il raggio di luce percorre avanti e indietro un tratto lungo d.

Se l’orologio è fermo, oppure si muove a velocità molto più bassa della velocità della luce, il percorso del raggio luminoso è proprio quello di figura 1. E quando dico “molto più basse” includo anche il mezzo più veloce attualmente costruito dall’essere umano, lo SpaceX che a noi può pure far impressione per la sua enorme velocità ma solo perché la riferiamo al nostro quotidiano, alle velocità dei mezzi di trasporto come treni e aerei. Tuttavia lo SpaceX compie una rotazione completa intorno alla Terra ad un’altezza dal suolo fra 300 e 500 km in circa 92 minuti, sicché viaggia alla mirabolante velocità rispetto al suolo di circa 28.000 km/h. E per quanto questa velocità ci possa far impressione, è una bazzecola rispetto a quella della luce che, ripetiamo, è di 300.000 chilometri al secondo. Questo significa che il nostro orologio, posizionato sulla Terra oppure a bordo dello SpaceX si comporta all’incirca allo stesso modo, generando un tick-tock ogni:

Ora proviamo a pensare cosa succede se l’orologio è invece a bordo di una fantastica astronave spaziale, come quelle dei film, in grado di muoversi a velocità paragonabili a quella della luce. Chiamiamo v la velocità dell’astronave.

In questo caso, mentre il raggio di luce sale verso lo specchio, tutto quanto si sposta nella direzione del moto, il raggio stesso e l’intero orologio, come visibile in Figura 2 che contiene vari “fotogrammi” dello stesso orologio, catturati a successivi istanti di tempo:

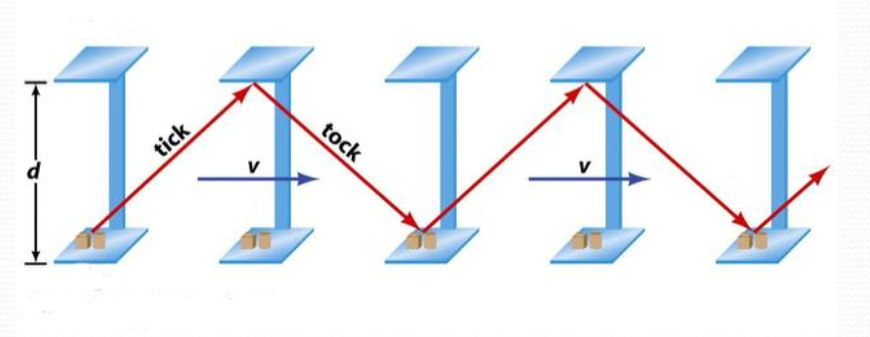
Figura 2: ecco cosa succede quando l’orologio si sposta verso destra ad una velocità v. Il raggio di luce e l’intero orologio si spostano considerevolmente durante ogni singolo tick-tock.

Cosa cambia rispetto alla situazione precedente?

La differenza più eclatante è che ora il raggio di luce percorre una distanza ben maggiore di quella che percorre quando l’orologio è in quiete. Cerchiamo di capire di quanto aumenta il percorso rispetto al precedente che, ricordiamo era due volte d.
Per capirlo riferiamoci alla figura 3, in cui usiamo la semplice formula del cartello stradale per ricavare gli spostamenti del fascio di luce e della struttura dell’orologio.

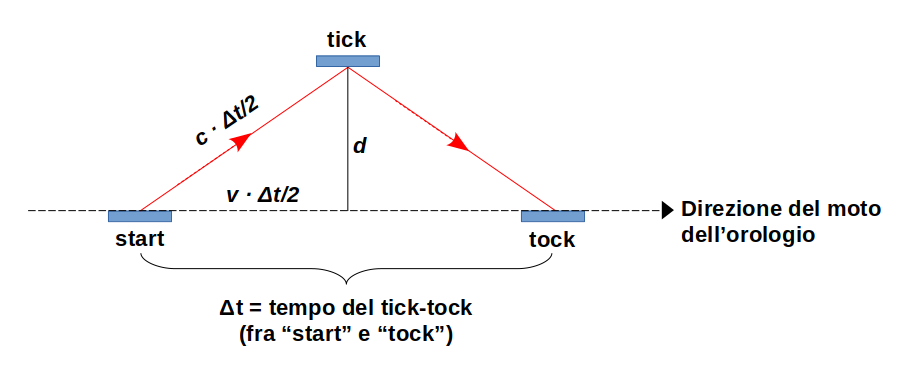
Figura 3: durante lo spostamento dell’orologio il fascio percorre due volte un tratto 

Qui facciamo uso del secondo postulato di Einstein: il fascio di luce ha sempre e comunque velocità c, sicché tra lo “start” e il “tick” percorre un tratto pari a velocità per tempo, dove il tempo è mezzo tick-tock.
Nello stesso intervallo, l’orologio, che invece viaggia a velocità v, si è spostato di conseguenza. Non è difficile vedere che si forma un simpatico triangolo rettangolo di cui conosciamo la lunghezza di ogni lato. Usando semplicemente il teorema di Pitagora si dimostra che il nuovo tick-tock è decisamente pià lento di quando l’orologio era in quiete, proprio come il buon senso ci indicava vedendo che il fascio di luce non va più su e già in verticale, bensì percorre un tratto diagonale in su e uno opposto in giù, che è ovviamente ben più lungo di due volte d (tratti rossi della Figura 3). Precisamente, il nuovo tick-tock rispetto a quello in quiete è più lungo di un fattore pari a:

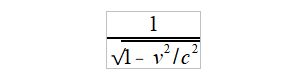
Se ad esempio l’astronave viaggia ad una velocità v=0.9 c, allora il tempo rallenta di un fattore pari a 2.3. Questo significa che se si viaggia a velocità prossime a quella della luce, il tempo si dilata, i tick-tock rallentano, il tempo scorre più lentamente.
Se si arriva molto prossimi alla velocità della luce, il tempo quasi si ferma e se fosse possibile viaggiare proprio a quella velocità, il tempo si fermerebbe proprio del tutto.

Le implicazioni di questo in Fisica sono moltissime, ma anche quelle sul nostro vivere quotidiano sono numerose. Ad esempio il sistema satellitare per la geolocalizzazione GPS ha implementato correttivi sulla misura del tempo per fornire dati a terra ad elevatisima precisione.

Marco Sartore