L’importanza della punteggiatura… una piccola virgola riesce a trasformare un avverbio interrogativo in un sostantivo, il Quanto, che il vocabolario Treccani definisce così: “Termine usato per indicare la «quantità» indivisibile, il valore più piccolo fisicamente possibile di una data grandezza variabile con discontinuità”. Stiamo parlando dunque di quella branca del sapere chiamata ‘Quantistica’ e venuta alla ribalta ai primi del ‘900 non appena gli studiosi si affacciarono alla finestra dell’infinitamente piccolo.

Erano quelli i tempi in cui una parte stolta e malefica dell’umanità metteva in campo le condizioni storiche per innescare i due conflitti mondiali, portando morte e distruzione, ma paradossalmente erano anche i tempi in cui un’altra fetta di umanità saggia e preparata iniziava un avanzamento nella Conoscenza pari o forse superiore solo a quello del Rinascimento. Questi due mondi in pieno contrasto correvano su binari paralleli, un po’ come avviene oggi quando sulla ISS, la stazione spaziale orbitante, convivono fraternamente scienziati di ogni dove mentre a pochi chilometri da loro, sulla crosta terrestre, altri umani con le loro stesse origini si fanno la guerra: stolta umanità.

La Quantistica di solito fa paura soprattutto quando associata alla Fisica, chi ne sente parlare o ne legge molto spesso si ferma al titolo. Nella speranza che qualche audace voglia andare oltre, cercherò di disegnarne solo i lineamenti, senza addentrarmi nelle cose difficili, ma offrendo un quadro scientificamente corretto.
La Scienza da sempre cerca di capire il mondo. Personaggi coraggiosi hanno dovuto faticare e a volte pagare con umiliazioni e angherie o con la vita per far accettare nuove verità, come ad esempio Niccolò Copernico e il suo eliocentrismo, che fu di una scomodità enorme per l’apparato ecclesiastico europeo contraddicendo uno dei suoi dogmi più importanti, quello secondo cui era il Sole a ruotare intorno alla Terra. E così come Copernico osservando un semplice tramonto intuì che in realtà era la Terra a ruotare intorno al Sole, un altro grandissimo Scienziato di nome Ludwig Boltzmann osservando un semplice bicchiere d’acqua intuì un brulicante fermento di piccolissime strutture, gli atomi. E fu proprio dai primi del ‘900 che si indagò sulla struttura di queste particelle a cui non venne cambiato nome nonostante si fosse scoperto che erano composte di oggetti più piccoli. Per inciso, a questo punto si sarebbe dovuto cambiar loro il nome perché ‘atomo’ deriva dal greco a + tomos, (alfa privativo + ‘tòmos’) ovvero ‘non ulteriormente divisibile’.

Ma divisibile l’atomo era eccome, secondo i primi modelli tra cui quello di Niels Bohr, il Fisico danese che propose un modello in cui un nucleo con carica positiva ma formato da protoni e neutroni ha intorno un certo numero di elettroni, con carica negativa, che ruotano su orbite circolari o ellittiche, come visibile in Figura 1:

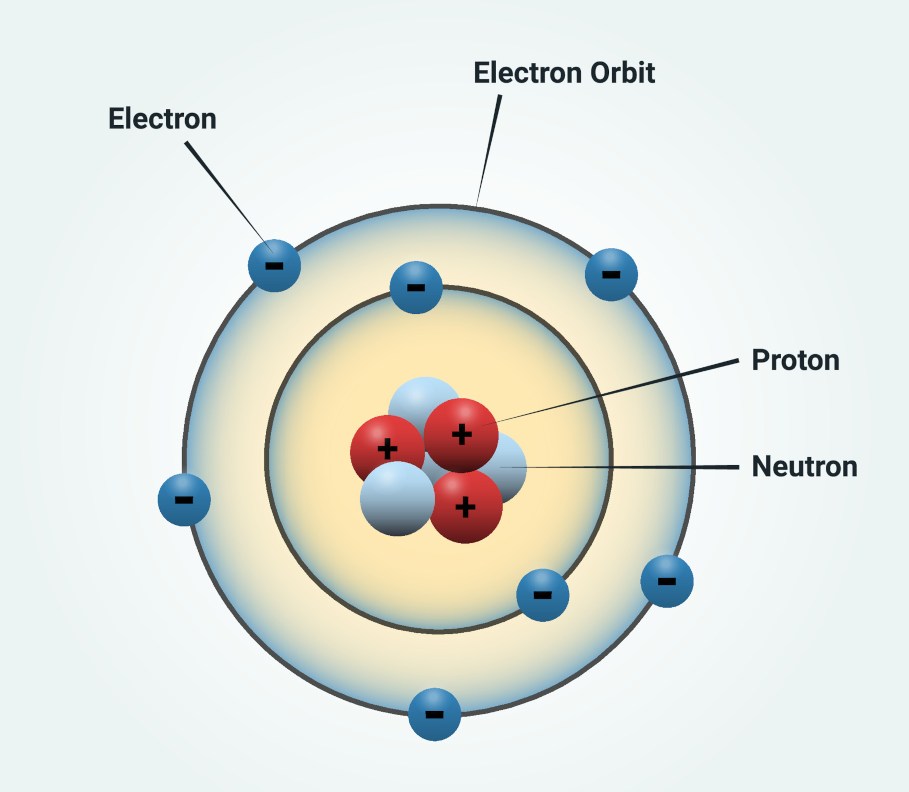
Figura 1. Rappresentazione grafica del modello di Bohr dell’atomo.

Sia chiara una cosa: sebbene il modello di Bohr possa essere visualizzato in modo davvero semplice, come in Figura 1 (allo stesso modo di altri modelli come quello di Rutherford, ad esempio), considerarlo “un disegnino” nato da una mente ispirata è sbagliato e quasi offensivo. Infatti la rappresentazione grafica è sempre figlia di una teoria sviluppata con le dovute formule matematiche che, come si può intuire per questo specifico argomento, risultano spesso molto complicate. Come dico sempre ai miei allievi, si fa presto a sminuire i risultati di uno scienziato se si tolgono dal contesto e dall’epoca in cui sono stati sviluppati. E li invito ad immaginare di aver davanti a sé un pannello nero impenetrabile al di là del quale si trova un atomo e, a disposizione per investigare l’ignoto, solo pochi antichi strumenti di misura: vista in questo modo la faccenda si complica e restituisce a questi precursori dei tempi la dignità che meritano.

La trattazione matematica di Bohr si sviluppò lungo una linea incredibilmente innovativa: le equazioni portavano a soluzioni secondo cui non tutte le orbite degli elettroni sono ammesse. Ad esempio, riferendoci ancora alla Figura 1, gli elettroni possono percorrere le due traiettorie circolari disegnate ma non una che sta in mezzo ad esse, oppure che è esterna alla più grande o interna alla più piccola.

Matematicamente ciò implica soluzioni discrete delle equazioni, cioè non più continue e lineari come nella Fisica del macro mondo. Questo risultato suonò strano innanzi tutti a Bohr stesso, che in un processo di autocritica forse troppo severa temette di aver sbagliato e non esitò a dichiarare che probabilmente le soluzioni discrete erano un artificio introdotto “per far tornare i conti”.

Non molto tempo dopo però Bohr capì che era tutto vero, ragionato e plausibile: le orbite ammissibili sono solo alcune e un elettrone, per passare da una all’altra deve acquisire o cedere pacchetti ben definiti di energia. Arrivò a questo risultato per via di una formula che qui riporto con l’unico scopo di discuterne la valenza innovativa:

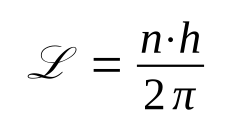
Qui L è il momento angolare dell’elettrone, h è la Costante di Plank (...costante, quindi valore fisso) e n è un numero che può valere 1,2,3...etc.

Quindi l’elettrone può assumere soltanto certi valori di L, non valori a piacere. E per la prima volta fece il suo ingresso il termine ‘numero quantico’, assegnato ad n.
Per spostarsi da un’orbita all’altra l’elettrone deve acquistare o cedere un’energia DE pari alla differenza delle energie delle due orbite interessate, assorbendo o emettendo una radiazione elettromagnetica di frequenza f anch’essa quantizzata e pari a:

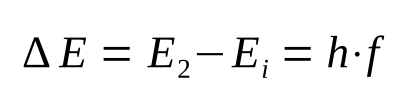
Si dice quindi che per cambiare orbita un elettrone deve acquisire o cedere un Quanto di energia.

Di solito piace questo paragone culinario: le superlative cuoche bolognesi mettono nell’impasto delle tagliatelle un uovo per ogni etto di farina. Quindi, 1 kg di farina, 10 uova. In Liguria le tagliatelle si chiamano “tajarin” e ai liguri piacciono un po’ più morbide (o più propriamente, un po’ più “lépeghe”), forse per condirsi meglio col pesto. Per questo mia nonna in 1 kg di farina metteva solo 7 uova. Ecco: le tagliatelle hanno un valore “quantizzato” di uova, 7 o 10 in questi due casi, ma non ad esempio 8.4 o 6.22: un uovo non si divide ulteriormente, o si mette o non si mette. L’uovo è il Quanto delle tagliatelle.

Se il nucleo dell’atomo di Bohr dimostra che un atomo non è “a-tomo” (indivisibile), i successivi contributi scientifici sono andati a studiare cosa dunque contenessero di ancora più piccolo, formulando una teoria fisica unitaria per tutto il micromondo nota come “Modello Standard”, quello oggi in uso.
Le vere particelle elementari o meglio particelle quantiche sono i Quark, ad oggi conosciuti come i costituenti più intimi della materia poiché non esistono evidenze sperimentali di sub-elementi o di strutture ancor più piccole.

In particolare, sia i protoni che i neutroni sono formati da 3 Quark, che stanno insieme grazie ad una delle quattro forze fondamentali, la Forza Nucleare Forte, come schematizzato in Figura 2:

Figura 2. Uno zoom sulla materia. A sinistra l’atomo, in centro il suo nucleo e a destra i quark che formano ciascun protone e neutrone.

I quark sono quanti di materia alla stessa stregua dei quanti di energia visti più sopra. Gli scienziati, che troppo spesso vengono additati come dei noiosi e cupi personaggi, sono spesso molto vivaci e fantasiosi, sicché nel descrivere le proprietà dei quark originate da seri calcoli e formule, nonché da teorie complesse e articolate, hanno attribuito loro “6 sfumature” (quark flavors) corrispondenti ai 6 possibili stati in cui si trovano, con nomi simpatici:

In particolare i protoni sono composti da uud e i neutroni da udd, cioè differiscono per un solo quark. Per loro quindi uno dei tre quark è decisivo nel decretare se la particella è protone o neutrone e si chiama ‘quark di valenza’.
Esistono altre particelle quantistiche, ed è curioso che i loro nomi finiscano sempre in “-one” come si usa fare nei suffissi accrescitivi (bicchierone = grande bicchiere), quando invece si tratta dei costituenti più piccoli e intimi della materia. Stiamo parlando di due grandi classi: i ‘leptoni’, di cui fanno parte ad esempio gli elettroni, e i ‘bosoni’, come ad esempio i fotoni luminosi.
Tutta questa pletora di componenti della natura ha un fattore comune: sono Quanti, particelle elementari.
Pensarli come palline che si muovono nello spazio aiuta a capirne essenza e natura, ma non fornisce una visione completa poiché i Quanti si comportano sia come particelle, sia come onde. E le cose iniziano a farsi intricate e meno intuitive, stiamo entrando nel mondo che li descrive esaurientemente e che si chiama Meccanica Quantistica.

Un esperimento famoso che decretò la parola fine all’allora diverbio se davvero un Quanto potesse essere contemporaneamente particella e onda fu quello della diffrazione degli elettroni. Immaginiamo di avere di fronte un pannello con due fenditure (due fori rettangolari) e di lanciare su di esso delle palline. È intuitivo capire che alcune rimbalzeranno indietro colpendo il pannello e alcune passeranno oltre quando riusciremo “a beccare” le fenditure. Se dietro al pannello teniamo traccia del punto dove arrivano le palline che riescono a passare, ci aspettiamo due strisce in corrispondenza delle due fenditure e in effetti questo è ciò che avviene usando le palline.
Se invece di oggetti discreti, ciò che colpisce le due fenditure è un’onda, le cose cambiano. Come le onde del mare quando attraversano una barriera frangi flutti aperta formano semicerchi che interferiscono con quelli vicini (Figura 3-a), così anche le altre onde al di là delle fenditure subiscono il fenomeno della diffrazione e formano frange multiple (Figura 3-b). Ciò sorprendentemente avviene anche bersagliando le due fenditure con un fascio di elettroni, che se da un lato sono di sicuro particelle come la Fisica ha ampiamente dimostrato, dall’altro esprimono comportamenti ondulatori.

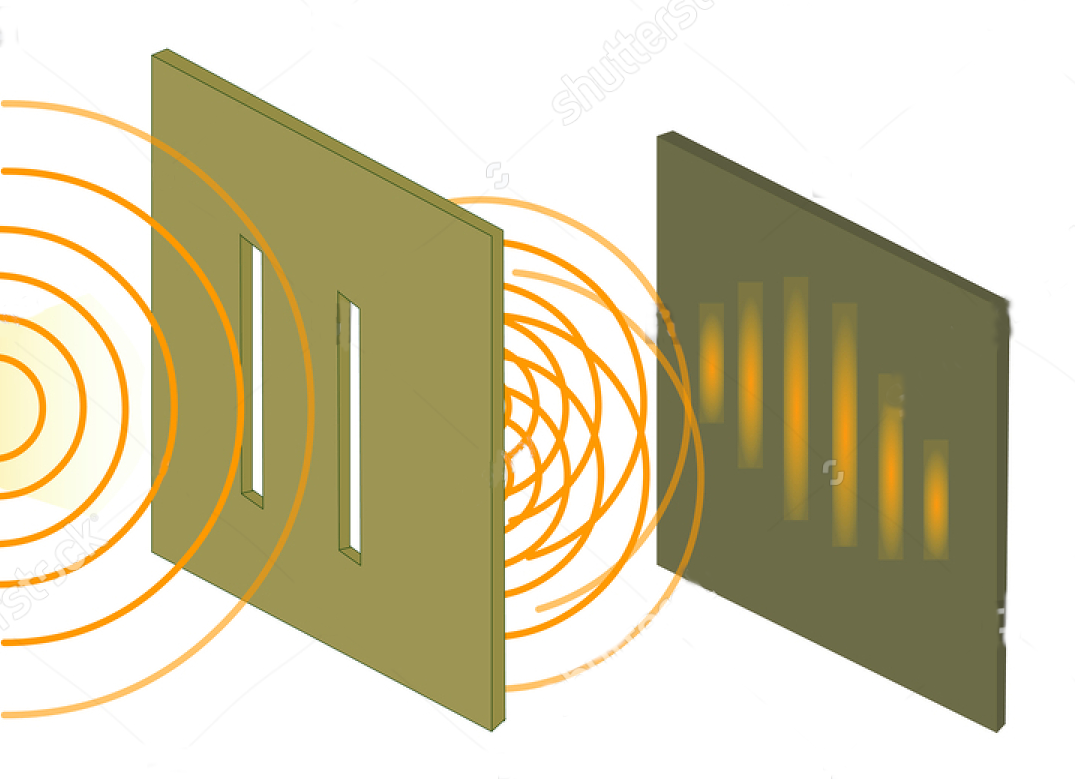
Figura 3. A sinistra (a) il fenomeno della Diffrazione di onde del mare che attraversano una barriera frangi flutti aperta in alcuni tratti, simili alle fenditure del pannello a destra (b) che quando colpito da un’onda forma sul muro posteriore identiche frange di diffrazione.

La Meccanica Quantistica descrive pertanto i Quanti come funzioni d’onda e riesce a prevedere i loro comportamenti con incredibile accuratezza. Questi comportamenti non sempre sono proprio intuitivi, anzi alcuni sono proprio lontani dalla logica che segue il mondo delle cose macroscopiche, quello in cui siamo abituati a vivere. Mi limito a citarne due, più per curiosità che per fornire un quadro completo sull’argomento, che sarebbe impossibile fare in modo così stringato.
Siamo abituati a distinguere nettamente due condizioni di un oggetto, ad esempio un piatto può essere integro oppure rotto, un pallone di colore bianco o rosso, e così via. In qualunque momento noi osserviamo l’oggetto, ne scopriamo immediatamente la caratteristica, senza ombra di dubbio cioè con probabilità 100%. Ebbene, questo non è più vero nel mondo dell’estremamente piccolo: un Quanto può essere contemporaneamente in uno stato o in un altro, ad esempio ruotare in senso orario o antiorario. Questa bizzarra caratteristica viene definita ‘sovrapposizione degli stati’.
Quando un osservatore esterno cerca di misurarne la proprietà, in quell’istante la fissa, la blocca e questa operazione di misura disturba il sistema che non è più in grado di ritornare nella sua sovrapposizione di stati precedente. È evidente quindi che “misurare” lo stato di una particella quantistica è cosa ben diversa da prendere un righello e misurare la larghezza di un foglio, che dopo la nostra misura rimane sempre il foglio che era prima.
Un facile esempio è pensare a un ipotetico Quanto che esiste in tre possibili stati corrispondenti ai tre colori azzurro, giallo e magenta come i vetri di figura 4:

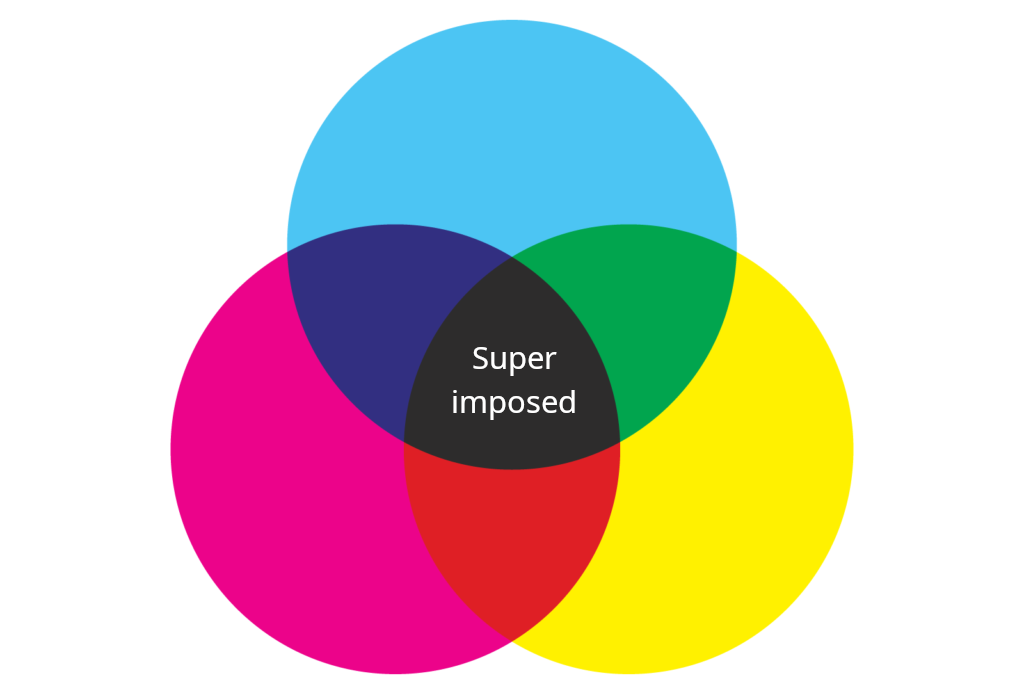
Figura 4. Sovrapposizione di stati esemplificata con 3 vetri colorati. La particella quantistica vive e appare come la zona al centro dell’immagine, possedendo contemporaneamente i 3 stati azzurro, giallo e magenta.

Quando decidiamo di misurare in quale stato la particella si trovi, il sistema “si congela” in uno dei tre colori, quello posseduto con probabilità maggiore nell’instante della misura.
Tutto questo è descritto dalla funzione φ, la ‘funzione d’onda’ del Quanto appunto, che contiene tutte le informazioni sulla probabilità che quella particella si trovi in uno stato piuttosto che in un altro. Dunque nella Meccanica Quantistica “misurare” significa richiedere a questa funzione informazioni circa la probabilità di una determinata proprietà della particella: il suo stato, il suo verso di rotazione, la sua velocità, etc.
La matematica che sta dietro alle funzioni d’onda è piuttosto difficile, ma a scopo puramente estetico vale la pena citare l’elegante Equazione di Dirac (il motivo sarà chiaro poco più avanti), un’equazione scritta nel 1928 da Paul Dirac che ha fatto la storia della Meccanica Quantistica e che descrive il comportamento di particelle quantistiche dotate di massa con spin ½, come ad esempio gli elettroni e i quark:

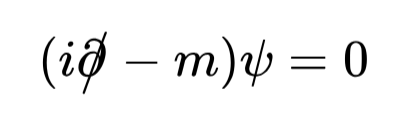
Ricordiamoci questa equazione e cosa descrive e passiamo senza indugi al secondo comportamento che voglio accennare: una particolare proprietà dei Quanti per cui due o più di essi possono essere creati indissolubilmente uniti, caratteristica che si chiama ‘entanglement’. Sostanzialmente, nel caso di due Quanti, funziona così: se nel momento in cui furono creati condividevano un certo stato, ad esempio entrambi avevano spin +1/2, una successiva misura fatta su una delle due particelle (che come visto sopra ne “fissa” lo stato) fissa anche lo stato dell’altra particella. E questo avviene anche se i due Quanti al momento della misura si trovano lontanissimi uno dall’altro.

Non sorprenderà quindi se all’entanglement è stato attribuito un significato molto romantico: due cuori uniti e complici, sia stando vicini che quando la vita li tiene forzatamente lontani. Probabilmente qualche Fisico quantistico costretto a studiare lontano dalla persona amata ha per primo pensato di accoppiare entanglement e amore, sta di fatto che si doveva a quel punto cercare un simbolismo da scrivere sui muri nei posti romantici come sull’Aventino o su magliette da condividere con la persona amata, come quelle di figura 5:

Figura 5. Le T-shirt dell’amore.

Ora, noi non romperemo l’incantesimo dicendo che l’Equazione di Dirac stampata sulle T-shirt non descrive assolutamente l’entanglement, un po’ come se per celebrare la rotondità della Terra avessimo scritto la formula del volume del cubo, e lasceremo che l’amore trionfi indisturbato al di là e al di sopra delle equazioni.

Concludo con un aneddoto fantastico che mi capitò in un bar a Marciana, dove un preparatissimo cameriere mi elencò tutti i tipi di birra disponibili e le relative pezzature, ad esempio, senza far pubblicità occulta: birra A, birra B, bicchiere da 0.2 o 0.3 o 0.4 litri, e così via. Dopo il lungo e articolato elenco alla fine scelgo birra X da 0.3 litri, pensando banalmente che un liquido potesse essere considerato un fluido continuo e, secondo la Fisica Classica, versato in un recipiente a piacere.
Ma niente Fisica Classica, fui immediatamente redarguito perché evidentemente avevo richiesto un livello energetico proibito, o uno stato quantico impossibile: la birra X ammetteva solo due stati, o 0.2 o 0.4 litri. E siccome 0.2 litri, come dice un famoso meme “è immorale”, optai infine per «birra X da 0.4 litri» che era una soluzione ammessa dell’equazione d’onda birraiola e bevvi con immensa soddisfazione pensando ad ogni sorso che si trattava della prima birra quantistica della mia vita.

Marco Sartore