Questo è un articolo colorato perché contiene molte figure che trattano di una questione antica come il mondo, giacché la prima ad occuparsene fu proprio Madre Natura: come coprire nel migliore dei modi una superficie o un volume con tasselli non sovrapposti senza lasciare buchi. Lo ha dovuto fare nelle rocce, nei vegetali, sugli animali. L’argomento ha affascinato l’essere umano da quando nacque l’idea di costruire un muro artificiale usando blocchi di pietra regolari, fino ad arrivare ai giorni nostri quando la tassellatura di una superficie è utile per visualizzare e risolvere problemi computazionali. Recentemente la questione è tornata di grande interesse scientifico grazie ad un importante avanzamento in questo campo da parte di un gruppo eterogeneo di studiosi, come vedremo nel seguito.
La suddivisione del piano in regioni contigue non sovrapposte è utile ed importante nella gestione delle risorse. Un esempio tipico è la decisione di quali utenti allacciare a varie cabine di diramazione della rete elettrica. In questo caso, un primo criterio di scelta è quello della vicinanza: collegheremo a una certa cabina tutti e soli quegli utenti che sono più vicini ad essa che ad ogni altra cabina. Il problema si risolve molto bene nel caso di due sole cabine elettriche: la linea di separazione di chi va allacciato a una o all’altra è semplicemente la retta centrale perpendicolare a quella che passa per le due cabine:

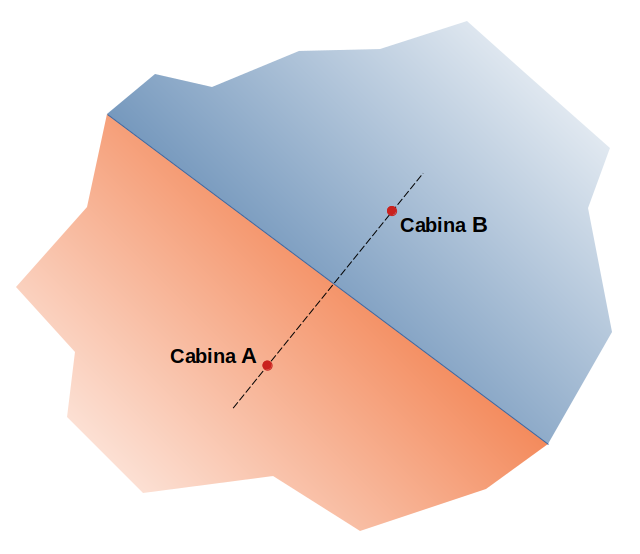
Figura 1. Le regioni colorate sono gli insiemi dei punti rispettivamente più vicini alle due cabine elettriche rappresentate dai pallini rossi.

Nella Figura 1, tutti i punti del piano della zona arancione sono più vicini alla Cabina A che alla B, viceversa quelli della zona azzurra. Poi resta inteso che l’allaccio potrà subire eccezioni legate a fattori contingenti, tipo la presenza di impedimenti geografici da qualche parte come montagne o fiumi. In questo caso l’algoritmo di assegnazione si fa più complesso e prevede l’introduzione di un peso proporzionato ad ogni vincolo progettuale, ma per questo hanno fabbricato gli Ingegneri ...e poi esula dall’argomento di questo articolo.
Se le cabine sono molte, il processo di suddivisione si può ripetere con la medesima regola di separazione. Quel che ne risulta è una segmentazione del piano che si chiama di Dirichlet–Voronoi [1], in cui si trovano n semi (‘seed’, corrispondenti ad esempio alle cabine elettriche) e in cui lo spazio è suddiviso in celle che rappresentano i punti più vicini ad un certo seed che ad ogni altro seed:

Figura 2. Una superficie quadrata segmentata con il metodo di Dirichlet–Voronoi.
I seeds sono i puntini neri e le celle hanno colori diversi.

Una caratteristica di questo tipo di mappe balza subito agli occhi: le zone in cui sono suddivise hanno lati dritti e angoli netti. Questi due aspetti hanno portato i matematici a creare altri tipi di tassellature utilizzando “mattonelle” simili.
Invece per coprire un piano con tasselli che si ripetono le soluzioni sono tante, basti pensare alla molteplicità di pavimenti disponibili. Utilizzando mattonelle esagonali, ad esempio, è possibile ricoprire l’intero piano e la struttura, se spostata di un modulo orizzontalmente o verticalmente, si ripete uguale a se stessa. Questo tipo di tassellatura viene quindi detta ‘periodica’:

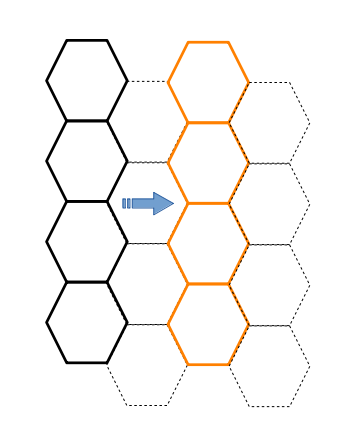
Figura 3. Tassellatura periodica del piano: il pattern di esagoni neri si ripete sovrapponendosi perfettamente a quelli arancioni. Lo stesso accade per gli altri esagoni presenti e anche spostando il pattern in verticale.

Ma a parte il piacere di osservare figure ordinate, artistiche e colorate, per quale ragione la tassellatura del piano ha suscitato interesse non solo negli artisti ma anche negli scienziati?
La ragione è che il problema è connesso intimamente a tutt’altra branca del sapere: i problemi decisionali, propri della teoria computazionale. Un problema decisionale è semplicemente quello che in base ad un input deve generare una risposta di tipo “si” o “no”, per esempio dato un numero il problema deve decidere se quel numero è primo oppure no. Ebbene, spesso il metodo decisionale può rifarsi alla tassellatura, indicando così una via risolutiva molto rapida ed efficace, sebbene inusuale.
Così numerosi studiosi a partire dagli anni ‘60 si dettero da fare per risolvere il seguente problema: qual è il minor numero di tasselli diversi necessario per ricoprire il piano senza lasciare buchi e in modo che la copertura sia NON-periodica (a-periodica) ?
Ovviamente dietro ad ogni soluzione visualizzata come un gradevole mosaico ci stanno pagine e pagine di calcoli geometrici, perché sia la costruzione del pattern che la dimostrazione della sua a-periodicità non sono affari semplici.
Chi diede una svolta sostanziale al problema fu intorno al 1974 Roger Penrose, matematico, fisico e filosofo della scienza, vincitore del premio Nobel per la Fisica nel 2020 (per tutt’altra motivazione: i suoi lavori sui buchi neri e la teoria della Relatività). Egli riuscì nell’impresa [2] utilizzando solo due tasselli, entrambi romboidali, con i quali peraltro è semplice costruire anche tassellature periodiche, ma che sapientemente posizionate danno origine alla copertura del piano a-periodica di Penrose, così importante e famosa che è stata riportata nel pavimento del Mitchell Institute for Fundamental Physics and Astronomy in Texas, dove lo scienziato insegna e lavora:

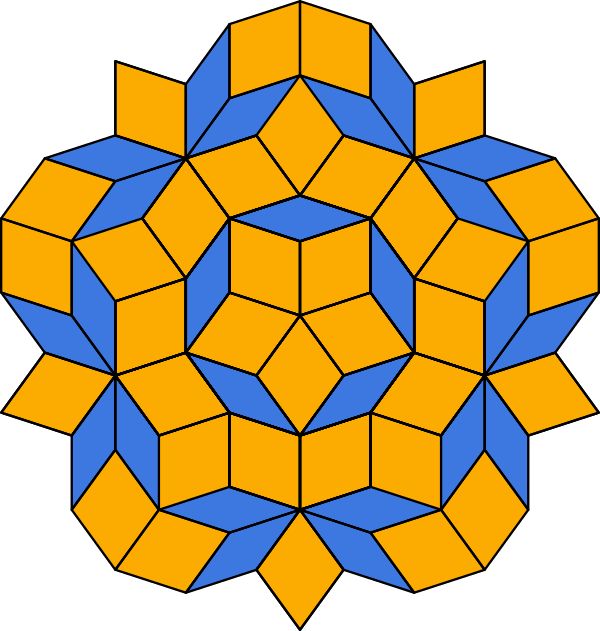
Figura 4. A sinistra una porzione della copertura del piano aperiodica a 2 tasselli e a destra il suo autore, Prof. Robert Penrose sul pavimento del Mitchell Institute in Texas che in suo onore è stato piastrellato con la famosa tassellatura.

In realtà Penrose prima di arrivare a questa soluzione derivò un buon numero di coperture, sempre aperiodiche, costituite da un maggior numero di tessere base. Tutte si sono rivelate utili soprattutto nello studio dei cristalli e degli insiemi di molecole [3].
È dunque due il numero minimo di tasselli con cui è possibile ricoprire un piano in maniera non-periodica ? Dagli anni ‘70 si è dovuto attendere fino al 2024 per capire che la risposta è no: esiste un tassello dalla forma molto particolare ed intrigante che, studiato mediante quella branca del sapere che si chiama Geometria Topologica, riesce nell’impresa facendo tutto da solo. Un bellissimo articolo [4] ha dimostrato che il tassello di Figura 5 completa la copertura di un piano creando strutture prive di alcuna ripetizione nello spazio bidimensionale. Questo tassello è stato chiamato ‘monotile’ (in inglese, leggasi dunque “monotail”):

Figura 5. Il ‘monotile’ di Smith, Myers, Kaplan e Goodman-Strauss.

Una caratteristica molto interessante di questo poligono apparentemente così bizzarro e spigoloso è che in realtà nasce dalla segmentazione di un ordinatissimo pattern di esagoni:

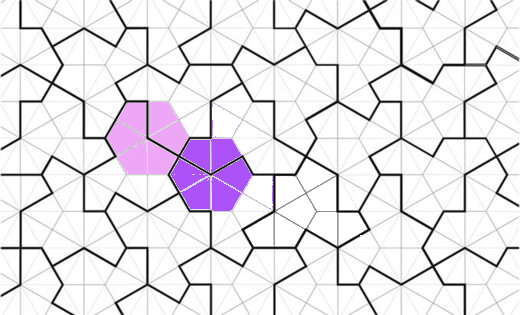
Figura 6. Il ‘monotile’ origina da un pattern esagonale, evidenziato qui sullo sfondo dell’intricato incastro. Per facilitare l’individuazione del pattern sottostante, due esagoni sono colorati di rosa e violetto.

Una curiosità... il tanto ricercato ‘monotile’ è noto anche come ‘Einstein tile’ ma questa volta il premio Nobel Albert non c’entra nulla: “ein stein” in tedesco vuol dire “una (singola) pietra” e quindi ‘Einstein tile’ significa che la tassellatura è fattibile “con un unico pezzo”.
Al di là degli aspetti matematici e geometrici, il monotile aperiodico si è rivelato fondamentale nello studio dei così detti ‘quasi-cristalli’ (quasicrystals), una forma della materia con struttura atomica ordinata ma non ripetitiva. Ciò ha dato un impulso notevole alla scienza di questi materiali.

Tuttavia la natura che ci circonda difficilmente è composta da strutture con lati dritti e angoli acuti. Pensiamo ad esempio ai vegetali e agli animali che popolano il nostro pianeta, molto raramente possiamo scorgere in loro qualche analogia con i tasselli visti finora. Se qualche ripetizione esiste, è comunque basata su moduli dalle forme ben più dolci e lineari.
Questa è la considerazione alla base di un lavoro scientifico pubblicato recentemente [5] che introduce una nuova interessantissima classe di tasselli chiamati ‘soft cells’ (“elementi morbidi”, soffici, che si possono distorcere ed elongare, o curvarsi, presentando pochi o nessun angolo acuto).
Immaginando di utilizzare tasselli di gomma morbida anziché di pietra o legno, la forma delle facce e dei bordi può essere fortemente distorta.

Tuttavia se si impone alle parti che:

- né si rompano formando fori

-né si incollino tra loro creando super-tasselli

allora facce, bordi e punti adiacenti rimarranno tali e avremo ancora tasselli come quelli di partenza, soltanto distorti. I primi e i secondi hanno tra loro una relazione di deformazione e sono detti “combinatoriamente equivalenti”.

Grazie a questa trasformazione da ‘tile’ a ‘soft cell’ il numero di angoli acuti viene minimizzato e i segmenti diventano curve. Ciò è ben comprensibile osservando la Figura 7a, che riporta la tassellatura del piano ottenuta con gli equivalenti combinatori del rettangolo, mentre la parte 7b richiama il quarto dei 5 pattern associandolo ad un paio di equivalenti in natura, la foce di un fiume e le cellule del tessuto muscolare:

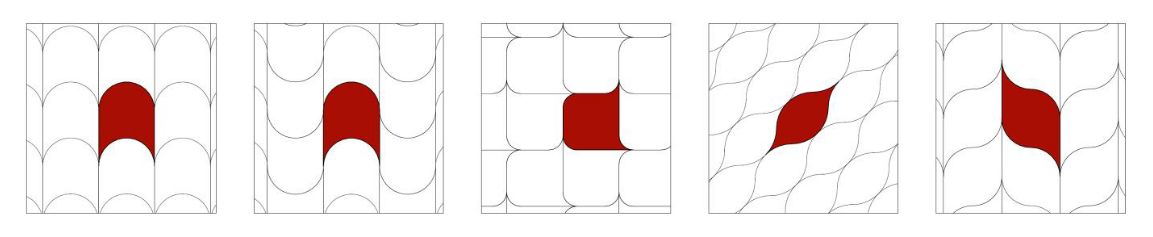
Figura 7. Sopra, parte A, le 5 possibili soft-cells generate da tasselli rettangolari. Sotto, parte B, due esempi di presenza in natura della quarta tipologia di soft-cell dell’insieme A.

L’appetito vien mangiando e gli autori non si sono limitati allo spazio bidimensionale, andando ad investigare il 3D. Dopo aver sviluppato un algoritmo per la curvatura degli spigoli, hanno creato le soft-cells 3D corrispondenti ai poliedri più comuni, sempre con lo scopo di descrivere elementi presenti in natura in maniera più accurata di quanto non sia possibile fare con gli spigolosi tasselli 3D classici.
La figura 8 mostra nella riga in alto i poliedri di partenza e in quella in basso le corrispondenti soft-cells tridimensionali:

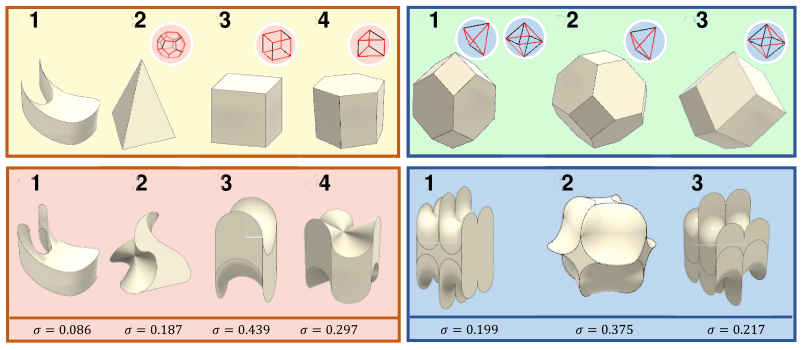
Figura 8. Suddivisi per numero di facce, in alto poliedri classici e in basso le corrispondenti soft-cells.

Il parametro sigma presente in figura è detto ‘softness’ e a grandi linee rappresenta il grado di deformazione del poliedro originale. È pertanto possibile modulare linearmente la curvatura di una soft-cell. che detta in un altro modo significa che da un poliedro si possono generare infinite soft-cells la cui forma è identica ma il cui grado di curvatura e morbidità è variabile a piacere. Quest’ultima caratteristica è molto utile quando si cerca di applicare la tassellatura 3D ad elementi reali naturali, poiché permette di adattare i tasselli mantenendone la forma e variando solamente le dimensioni.
Un esempio molto bello, con il quale concludo, è il modello tridimensionale del famoso Nautilus (Nautilus belauensis), sul cui legame con la ‘sezione aurea’ ho scritto diffusamente nel mio libro “Mirabilia maris” [6]. La sua struttura è composta da moduli sovrapposti che sono stati esattamente riprodotti mediante soft-cells:

Figura 9. A sinistra in alto l’immagine in trasparenza di un Nautilus ai raggi X e super-imposta la soft-cell che lo modella, riportata nella sua versione di partenza in basso. A destra l’intero guscio ricostruito con tassellatura 3D.

In conclusione possiamo certamente affermare che è stato necessario attendere fino al 2024 per avere soluzioni definitive a problemi che, come abbiamo visto ad inizio articolo, sembrano di facile soluzione. La difficoltà principale dal punto di vista matematico e geometrico sta nel dimostrare in modo inequivocabile le proprietà di una certa tassellatura, prima fra tutte la sua a-periodicità. L’importanza dei problemi di tassellatura, invece, trascende gli aspetti matematico-geometrici poiché queste strutture sono sorprendentemente utili per districare problemi decisionali in informatica e di gestione delle ‘risorse di sistema’ in ingegneria.

Marco Sartore

References

1. "Computing Dirichlet tessellations", A. Bowyer, Computational Journal 24 (2): 162–166 (1981). https://doi.org/10.1093/comjnl/24.2.162

2. "Pentaplexity: A class of non-periodic tilings of the plane", R. Penrose, The Mathematical Intelligencer. 2: 32–37, (1979–80). https://doi.org/10.1007/BF03024384

3. "A simpler approach to Penrose tiling with implications for quasicrystal formation", Steinhardt, Paul J.; Jeong, Hyeong-Chai, Nature 382: 431–433, (1996). https://doi.org/10.1038/382431a0

4. “An aperiodic monotile”, David Smith, Joseph Samuel Myers, Craig S. Kaplan e Chaim Goodman-Strauss, Combinatorial Theory 4 (1) (2024), #6

5. “Soft cells and the geometry of seashells”, G. Domokos, A.Goriely, Á. G. Horváth and K. Regős, PNAS Nexus, 2024, 3, pgae311, https://doi.org/10.1093/pnasnexus/pgae311

6. “Mirabilia Maris – Le meravigliose forme del mondo sommerso”, Marco Sartore, Edizioni IRECO, https://ireco.net/prodotto/mirabilia-maris/