È molto affascinante constatare che in molti casi la soluzione di un problema è basata su idee semplici, così semplici che vien da dire “Ma perché non ci avevo pensato io?”. Questo sentimento nasce in noi perché riusciamo a capire benissimo la soluzione, essendo appunto non complicata, ma solo grazie al fatto che una mente brillante l’ha ideata prima di noi, rendendocela disponibile. Ho deciso di celebrare questo ‘pensiero semplice’ raccontando tre diverse idee geniali con l’intento positivo di stimolarci ad affrontare le prossime sfide personali con ottimismo, andando a cercare la soluzione più semplice ...che quasi sempre è anche la migliore.

A cavallo fra il 1700 e il 1800 in una piccola scuola di Brunswick, nella bassa Sassonia, una maestra elementare doveva correggere i compiti dei propri alunni, che cominciarono a fare un gran baccano trovandosi esenti da spiegazioni e compiti. La maestra tentò quindi di placare gli animi assegnando alla classe un compito apparentemente noioso, scelto apposta per ritagliarsi una mezz’oretta di pace e sentenziò: “Calcolate la somma dei numeri da 1 a 100”.

A pensarci bene, è una cosa davvero noiosa: 1+2=3, poi avanti: 3+3=6, etc come in Figura 1:

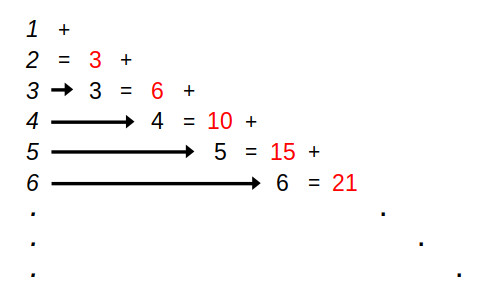
Figura 1. Come la maestra pensava si sarebbe svolto il compito assegnato.

La sfortuna (si fa per dire) della maestra fu che nella sua classe era presente il giovane Carl Friedrich Gauss, un bambino che stava per rivelare al mondo la propria eccezionale intelligenza: dopo soli cinque minuti si presentò alla cattedra e disse: “Ecco Maestra, ho fatto il compito”. Ovviamente l’insegnante tentò di rimandarlo a posto sentendosi presa in giro, ma dopo l’insistenza dell’alunno scrutò quel foglietto e rimase sbigottita, la risposta era corretta ma soprattutto il metodo usato era sbalorditivo.
Gauss ebbe l’abilità di “vedere” tutti insieme i numeri che precedono il 100, di fila uno all’altro. Capì così che il primo e l’ultimo numero della serie (1 e 99) sommati fra loro facevano proprio 100. Ma anche il secondo e il penultimo (2 e 98), e così via:

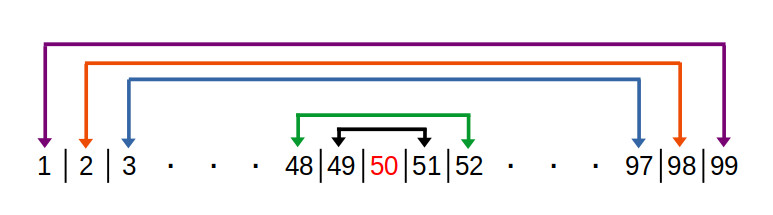
Figura 2. Raggruppamento dei numeri da 1 a 99 per formare somme pari a 100.

Questa cosa si ripete per tutti i numeri da 1 a 49, mentre il numero 50 rimane “da solo”, per questo colorato in rosso in Figura 2, sicché per 49 volte si ha come risultato 100 a cui non rimane che sommare il residuo 50 ...e il 100 finale a seconda che sia considerato incluso o meno nel problema (ciò significa che è diverso chiedere “la somma dei numeri da 1 a 100” oppure “la somma dei primi 100 numeri”, nel secondo caso si parte da 0 e ci si ferma a 99):

Il metodo funziona con qualunque numero finale al posto di 100, con la sola differenza che ‘il numero centrale’ è presente solo per quelli pari.
Quando l’insegnante capì le abilità intellettuali di Gauss, che era di famiglia modesta, lo presentò al Duca di Brunswick il quale lo supportò economicamente e gli fece frequentare il locale ‘Collegium Carolinum’. Questo fu l’inizio di un percorso fantastico che portò infine il geniale Gauss a insegnare all’Università di Göttingen e a fare innumerevoli scoperte in ambito scientifico. I Fisici e gli Elettronici lo conoscono soprattutto per i suoi studi sul flusso del campo elettrico, ma i suoi risultati furono ben più numerosi ed intriganti. A me piace una sua frase, che ho fatto mia e che con infinita modestia perseguo da sempre in modo del tutto naturale: “Non è la conoscenza, ma l’atto di imparare, non è il possedere, ma l’atto di essere là che garantisce il più alto piacere. Quando io ho compreso ed esaurito un argomento, scappo da lui in modo da rituffarmi nel buio”.

Andando molto indietro nel tempo, fino al 200 a.C. circa, troviamo Eratostene, grande scienziato dell’epoca che dette inizio alla moderna trigonometria ma che è soprattutto noto nel campo aritmetico per aver elaborato il famoso “Crivello di Eratostene”, un metodo per individuare i numeri primi che ogni studente di Informatica o di Ingegneria non può fare a meno di implementare almeno una volta nella vita durante i suoi studi.
Usando solo la propria mente geniale e uno stecco di legno, Eratostene riuscì a calcolare la circonferenza della Terra, verificando al contempo che è “sferica”, purtroppo per i terrapiattisti (uso le virgolette perché oggi sappiamo che non è una sfera perfetta, essendo un po’ schiacciata ai poli).
Eratostene osservò che nella città egiziana di Syene, l’odierna Assuan, a mezzogiorno nel solstizio d’estate uno stecco piantato verticalmente nella sabbia non creava alcuna ombra. Ciò significa che in queste condizioni e in questa posizione geografica il sole è esattamente perpendicolare al terreno.
Spostandosi ad Alessandria d’Egitto, sempre a mezzogiorno nel solstizio d’estate, Eratostene osservò che quello stesso stecco piantato perpendicolarmente nella sabbia formava una piccola ombra. Misurò allora l’angolo α fra lo stecco e la linea d’ombra, come in Figura 3 seguente:

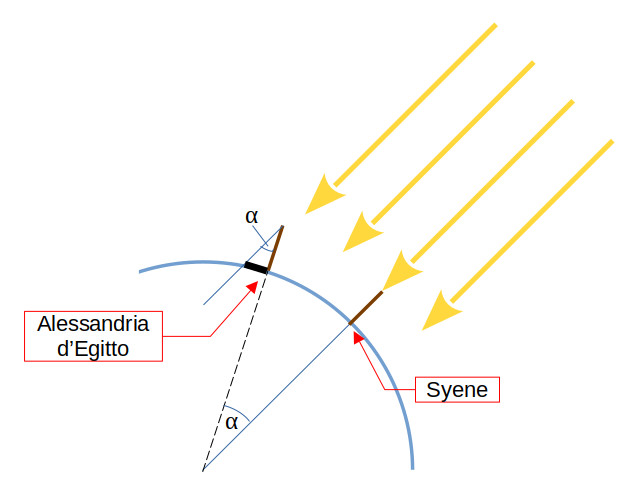
Figura 3. L’angolo al centro della Terra compreso fra le città di Syene e di Alessandria d’Egitto è uguale a quello fra lo stecco e la propria ombra.

Eratostene fece numerose ed accurate misurazioni, come testimoniato dagli scritti di Cleomede, matematico e astronomo, anche in luoghi lungo la linea che tocca le due città. Alla fine constatò che l’angolo era di 7.2°, pari ad un cinquantesimo dell’angolo giro.
Supponendo che la Terra sia una sfera perfetta, in cui l’angolo giro di 360° descrive una sua qualunque circonferenza, Eratostene arguì che l’angolo misurato doveva corrispondere in proporzione alla distanza fra Syene ed Alessandria d’Egitto, secondo la seguente uguaglianza:

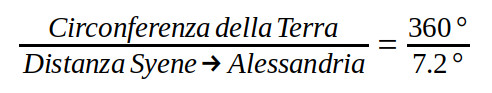
La distanza nell’antico Egitto aveva come unità di misura gli “stadi” (1 stadio corrisponde a circa 160m) e quella fra le due città è di 5000 stadi, pertanto:

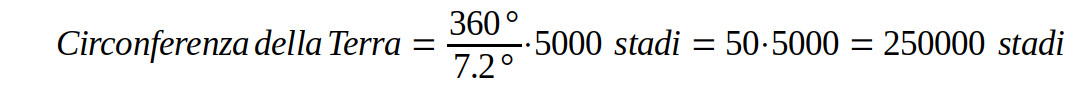
Tradotto nell’odierna unità di misura, il calcolo di Eratostene della circonferenza della Terra porta ad un risultato pari a 250000 · 160 m = 40000 km.
La misura precisa della circonferenza polare, calcolata oggi con l’ausilio di satelliti e di tecniche di misura estremamente sofisticate, è pari a 39941 km !
Il confronto dei due numeri non ha bisogno di altri commenti per lasciarci senza parole di fronte alla grandezza di un’idea semplice elaborata da una mente geniale. Il metodo di Eratostene è una applicazione brillante di geometria di base unita ad osservazioni sperimentali per risolvere un problema complesso. Ha dimostrato la potenza del ragionamento e del pensiero scientifico già in tempi antichi e ha posto le basi per innumerevoli future misurazioni riguardanti il nostro pianeta.

Passiamo infine al teorema forse più famoso e noto al mondo: quello di Pitagora. Sebbene a molti faccia venire in mente la Grecia, paese di nascita dello scienziato, la scuola Pitagorica nacque e si insediò qui in Italia, precisamente a Crotone, poiché la Calabria nel sesto secolo a.C. era parte della Magna Grecia.
I Pitagorici basavano le proprie attività sullo studio e sulla condivisione del Sapere, riuscendo anche a modellare la vita sociale della città e dei dintorni dove la scuola si espanse ben presto.
Il noto teorema dice che in un triangolo rettangolo la somma dei quadrati dei cateti è pari al quadrato dell’ipotenusa. Ciò implica che i tre lati di questa figura geometrica che possiede un angolo di 90 gradi non possono avere lunghezze qualunque, bensì legate dalla relazione appena citata. Ciò vale per lati di qualunque lunghezza, ma esistono anche triplette di numeri interi (cioè senza il punto decimale) che soddisfano la relazione Pitagorica, la più famosa delle quali è certamente [3,4,5].
Storicamente le triplette Pitagoriche erano note ben prima del sesto secolo a.C., in India e in Babilonia. Famosa è ad esempio la tavola di creta babilonese chiamata ‘Plimpton 322’ e visibile in Figura 4 che contiene 15 righe di numeri interi tutti formanti triplette Pitagoriche. I numeri sono scritti in modo non direttamente leggibile da noi, usando la tipica “scrittura cuneiforme” babilonese e, per di più, con numeri sessagesimali, cioè in base 60 (oggi noi usiamo normalmente la base 10):

Figura 4. Il Plimpton 322 riportante 15 triplette pitagoriche.

Ma fu Pitagora a razionalizzare le conoscenze pregresse a lui pervenute con tutta probabilità dall’Oriente quando ancora abitava in Grecia e a trovare la relazione quadratica fra i lati del triangolo rettangolo.
Sebbene nessuno scritto sia giunto a noi riportante la testimonianza certa di come Pitagora riuscì a dimostrare il teorema che porta il suo nome, l’ipotesi più accreditata in base ai reperti storici è che lo scienziato ebbe un’idea molto semplice per farlo, costruendo due identici quadrati e disponendo diversamente al loro interno quattro identici triangoli:

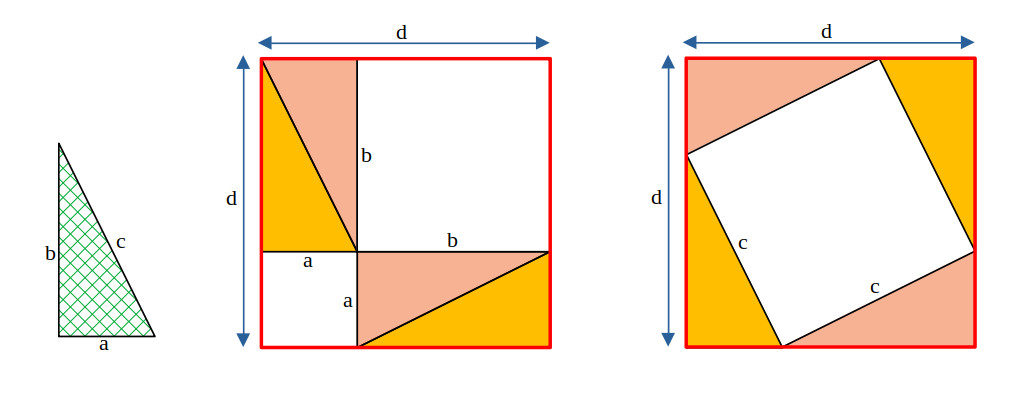
Figura 5. Dimostrazione geometrica del Teorema di Pitagora.

I due quadrati rossi di lato d e quindi di pari area contengono entrambi lo stesso numero di triangoli (quattro), identici a quello zigrinato in verde a sinistra. La parte di superficie dei quadrati ‘occupata’ dai triangoli è quindi la stessa nei due casi. Ne consegue quindi che il resto della loro superficie, bianca in figura, deve essere pure la stessa nel quadrato rosso a sinistra e in quello a destra.
Nel primo la superficie bianca è formata da due quadrati più piccoli, rispettivamente di lato a e b, mentre nel secondo è formata da un unico quadrato di lato c, pertanto:

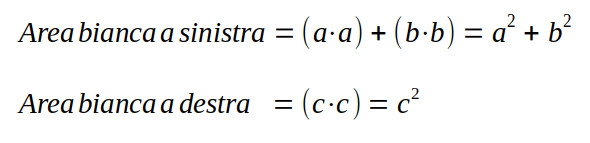
Ecco quindi dimostrato geometricamente il teorema, per semplice ‘riempimento’ delle zone lasciate vuote dai quattro triangoli:

Questi sono solo tre esempi fra i molti che utilizzano idee molto semplici per risolvere problemi complessi e portano a pensieri quasi filosofici sulla realtà e sulla sua descrizione matematica che gli umani hanno prodotto per misurarla e conoscerla. La nostra è davvero la matematica migliore o ‘giusta’ per fare i conti col mondo che ci circonda, dall’infinitamente piccolo alle distanze siderali? Oppure ci siamo complicati la vita con la formalizzazione attualmente in uso e ne esisterebbero di più semplici?

Sta di fatto che agli interrogativi più grandi ancora aperti non solo non abbiamo trovato modo di dare una risposta, ma ci siamo incamminati verso una formalizzazione matematico-fisica così complicata che ci viene invidia per la semplicità delle grandi menti che ci hanno preceduto, soprattutto se raffrontata alla grandezza dei loro successi scientifici.

Marco Sartore