Dodici mesi son passati e questo numero risuona forte nella nostra mente, si chiude un ciclo e se ne apre uno nuovo. Ma perché proprio 12 sono i mesi e non ad esempio 10 come la base dei numeri che usiamo ogni giorno “per far di conto”?
Nell’antica Mesopotamia esisteva fin verso l’ottavo secolo a.C. il popolo dei Caldei, fra i primi a studiare il cielo. Fra le altre scoperte fu proprio quel popolo a notare che il percorso del sole rispetto alla terra era ciclico e toccava 12 costellazioni, rimanendo in ciascuna di esse all’incirca 30 giorni per poi spostarsi alla successiva ed infine, dopo averle toccate tutte, ripartire dalla prima.
Dopo Copernico abbiamo imparato che quel percorso è solo virtuale poiché è la terra che ruota intorno al sole, tuttavia la posizione apparente del sole rispetto alla volta celeste è mappata lungo la linea chiamata “eclittica”, intersezione del piano orbitale terrestre con la “sfera celeste”. E proprio prendendo quest’ultima come sfondo si osserva che il sole ‘tocca’ le dodici costellazioni descritte per primi dai Caldei:

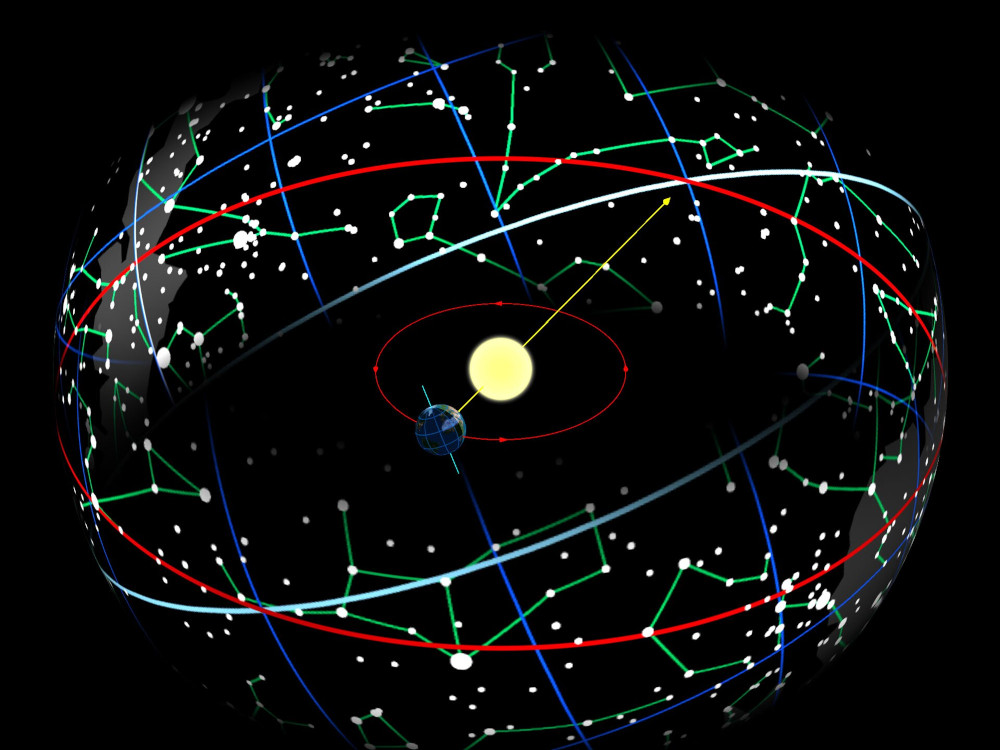
Figura 1. La linea rossa rappresenta l’eclittica solare ovvero il percorso apparente del sole per un osservatore posto sulla terra.

Rimanendo circa 30 giorni in ognuna e ripartendo dalla prima a fine percorso, i Caldei calcolarono che un anno durava 30 x 12 = 360 giorni: un’ottima approssimazione degli attuali 365, corretti ogni quattro anni dal bisestile.
Per inciso, grazie questa e a molte altre osservazioni del cielo i Caldei furono un popolo rispettato, venerato e temuto, in quando gli si ascrivevano capacità speciali di predizione del futuro. Furono studiosi attenti e meticolosi, come testimoniano le tavole di argilla in cui riportavano le osservazioni e calcolavano i cicli celesti. Verso l’ottavo secolo a.C. i Caldei si mescolarono alle altre popolazioni mesopotamiche perdendo la propria identità.
Da allora i mesi dell’anno sono sempre stati 12 e questo numero ha assunto un’importanza sempre crescente nel mondo, tanto che i primi conteggi non furono in base 10 come nella nostra numerazione classica, bensì in base 12 (a cui presto i Babilonesi affiancarono i numeri “sessagesimali”, cioè in base 60: pratici ma un po’ scomodi, visto che prima di arrivare all’equivalente decina bisogna assegnare 59 simboli differenti ai numeri, se escludiamo lo zero [1]).
D’altronde già in epoca romana il dodici aveva perso la prerogativa di base numerica di uso comune, come testimonia anche la sua etimologia latina duodecim, composto di duo «due» e decem «dieci». Un nome che parla di una modifica operata al numero importante, il 10, la cui indiscussa fama è certamente dovuta al fatto che noi umani abbiamo dieci dita e che usando quelle i calcoli e i conti sono facili da eseguire. Tuttavia il dieci non è sempre così comodo.
Se il dodici fece la propria apparizione per il citato motivo cosmologico, poi la sua importanza si è estesa nell’uso comune per un motivo del tutto diverso, ovvero per una ragione matematica molto pratica: il 12 è un numero “altamente composto”, cioè ha più divisori di qualsiasi altro numero intero positivo minore di lui. Come sappiamo, infatti, è divisibile per: 1, 2, 3, 4, 6, 12. Questa proprietà lo rende un numero molto utile nella vita di tutti i giorni.
Ad esempio, suddividere in tre parti in base 10 significa fare i conti con decimali infiniti: 1/3=0.333… mentre la stessa operazione in base 12 offre un ben più pratico 1/3=0.4. Ciò rende molto più facile dividere le dozzine che non i gruppi di dieci ed è forse per questo che ancora oggi le uova sono confezionate in gruppi di 6 o 12 … come sappiamo le ricette che ne fanno uso devono spesso essere frazionate per realizzare il medesimo piatto ma per un numero diverso di commensali e farlo con le decine risulterebbe ben più scomodo che partendo dalle dozzine.
Una simpatica conseguenza della cosa è infatti il calcolo frazionario, ad esempio la somma delle frazioni 1/3 e 1/4 in base 10 è davvero poco pratica:

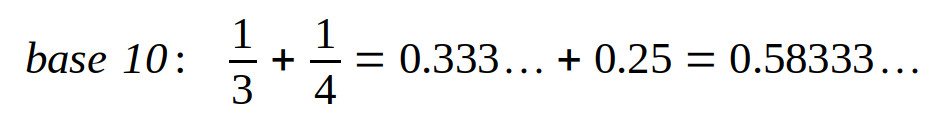
mentre in base 12 diventa meglio gestibile:

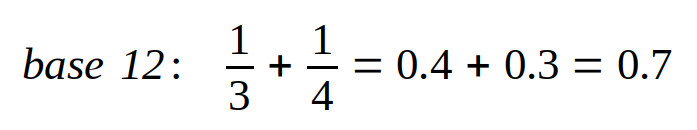
Se ad esempio abbiamo due dozzine di uova possiamo prenderne un terzo dalla prima, cioè 4 uova, e un quarto dalla seconda, cioè 3 uova, per un totale di 7.
Ragionare usando il 12 è una vera arte contadina … e non solo quando si parla di uova. Che ci si creda o no, l’uso di bottiglie da 0.75 litri per il vino e lo spumante deriva da quello. Infatti la tipica damigiana è da 54 litri e usandola per riempire bottiglie di questa capacità si scopre che ne servono esattamente 72. E 72 bottiglie di vino son molto comode da suddividere in 12 confezioni da 6 bottiglie ciascuna, molto comuni, oppure in 6 casse da 12 bottiglie ciascuna.
In matematica avanzata il 12 più famoso e scomodo è certamente quello tirato fuori dal cilindro da una delle più grandi menti in campo numerico, Srinivasa Ramanujan. Era un povero ragazzo autodidatta dei primi del ‘900 quando scrisse ad un certo Prof. Micaiah Hill di Londra una famosa lettera in cui dimostrava che la somma dei numeri interi positivi converge al valore -1/12 guadagnandosi da questo una sequela di insulti:

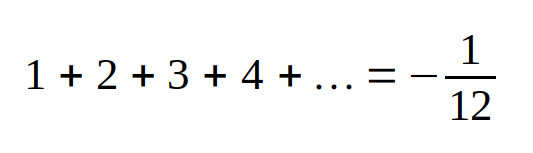
Ma il povero professore era la vera persona da insultare: Ramanujan aveva appena esplorato alcuni intriganti aspetti di una nuova matematica, la così detta “Analytic Continuation”, oggi legata strettamente alla descrizione di problemi di Fisica Quantistica. Se infatti non serve altro che il buonsenso per capire che nella “nostra” matematica la somma di un numero infinito di numeri positivi diverge all’infinito, una maggior modestia avrebbe scongiurato la figuraccia di Hill che non si accorse dell’eccellenza del proprio interlocutore, che stava aprendo le porte ad una nuova branca del sapere. Sta di fatto che quel 12 a denominatore fece scalpore al punto da spalancare al giovane Ramanujan le porte della prestigiosa Università di Cambridge, nel Regno Unito [2] ed oggi la convergenza della sommatoria dei numeri naturali positivi a quel -1/12 è diventata un’icona speciale.

In geometria il solido a 12 facce si chiama dodecaedro e per costruirlo si uniscono lungo i lati dodici pentagoni:

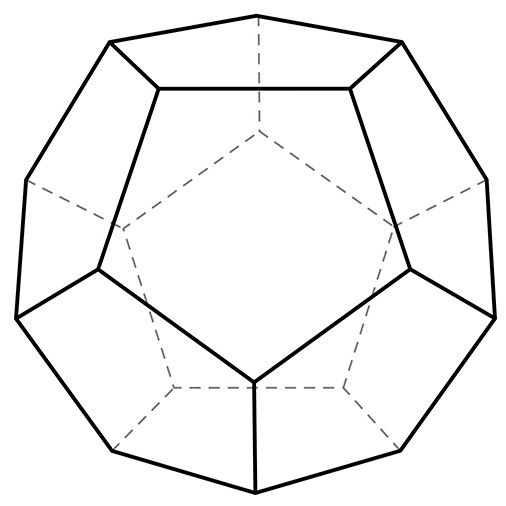
Figura 2. Il solido a 12 facce o Dodecaedro.

Invece il solido a 12 vertici si chiama icosaedro e per realizzarlo si uniscono fra loro venti triangoli:

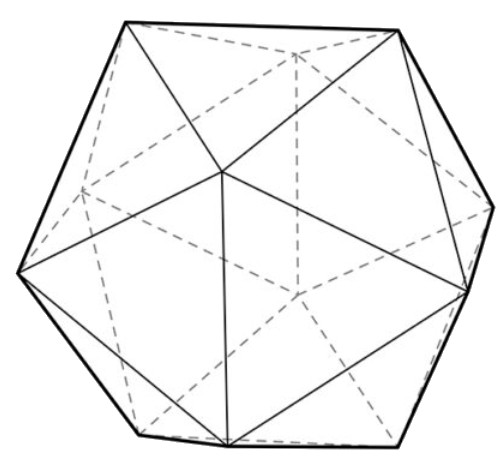
Figura 3. Il solido a 12 vertici o Icosaedro.

Il dodecaedro assunse grande rilevanza nei tempi antichi, a seguito della suddivisione dell’anno in 12 mesi operata dai Caldei, come visto all’inizio. Platone raffigurò con questa forma geometrica l’Universo, anche perché il dodecaedro può contenere in modo perfetto gli altri quattro solidi platonici che venivano associati ai quattro elementi: aria, acqua, terra e fuoco (questi sono il tetraedro o piramide triangolare, il cubo, l’ottaedro e, appunto, l’icosaedro) [3].
L’associazione fra il numero 12 e l’universo si ritrova anche in molte espressioni religiose, a partire dai 12 Dei dell’Olimpo, fino alle 12 Tribù di Israele degli ebrei, ai 12 Apostoli dei cattolici, ai 12 Imam degli islamici, alle 12 connessioni del ciclo dell’esistenza dei buddisti, alle 12 divinità legate all’energia del sole degli induisti.

Infine, il cerchio è suddiviso in 12 settori di trenta gradi per realizzare l’orologio, che divide il giorno in 12 ore antimeridiane e in 12 post meridiane. Questa convenzione pare nata nell’antico Egitto dove a dieci intervalli diurni vennero aggiunti i due relativi all’alba e al tramonto per un totale appunto di 12, a cui fu naturale accoppiare altrettante suddivisioni notturne.
Al legame del 12 con il cerchio è stato assegnato un simbolo di completezza e di unione e per questo motivo 12 sono le stelle poste in cerchio nella bandiera Europea.

Marco Sartore

Riferimenti bibliografici

1. “Il museo dei numeri”, Piergiorgio Odifreddi, Ed. Rizzoli (2014)

2. "On certain infinite series", Ramanujan, S. Messenger Math. 45: 11–15, (1915).

3. "Altitudes of a tetrahedron and traceless quadratic forms", Havlicek, Hans; Weiß, Gunter, American Mathematical Monthly. 110 (8): 679–693, (2003). doi:10.2307/3647851.